Overview

My father has a passion for crafting various things out of wood. He also likes puzzles and recently decided to make a bunch of 3x3 wooden cubes, 6-7 pieces each. Since he randomly chose the pieces shapes, of course I could find no solution online for any of the cubes. After trying, unsuccessfully 😊, to solve them for a few days, I decided to write my own generic solver.

Research

The first thing I had to figure out was how to actually plot 3D pieces and play with them in different positions - rotate and translatem then around. To generate a volumetric plot, I found out that matplotlib is actually really easy to use and well documented. After playing around with some code from the docs, I had a PoC that could create shapes and plot them together nicely with different colours.

Great! Now on to perform the different transformations. Translations are very easy - simply increase or decrease the x, y or z coordinates. For rotations, I used the basic rotation matrixes for 3 dimensions:

Next I did some research to see what other solvers are out there. The only other working one I could find is the Wooden cube C solver. Written in C, this is lightning fast and I quickly tested it against my 2 different cube configurations. It solved both of them instantaneously. Awesome! The code is very long (It’s written in C. Did I mention that already?), but very organised and well written. Because I in fact wanted to understand and learn something so I decided to code my own solver in Python.

This project has 2 main important chunks: generating all the possible transformations for each piece and them brute-forcing a solution. I tinkered a bit with a few iterations of the function that searches for a solution, and settled with a different variant but which I’ve optimised to perform well even on a high level language like Python, with the advantage that I got a much shorter code (less than 200 lines in total, including the graphics display functionaity), cleaner and easier to understand (I hope).

Coding

In terms of data structures, I opted for Numerical Python (aka NumPy) which are faster, more efficient, and require less syntax than standard Python lists. They are also more intuitive and easy to use for performing normal operations over matrices. More on this later!

I’m plotting the pieces as a list of 3D volumetric shapes:

# Plot a list of pieces with a volumetric 3D plot
def plotPieces(pieces):
    # Combine the pieces
    voxelarray = functools.reduce(lambda a, b: a | b, pieces)

    # Colour each piece
    all_colors = [name.split('tab:')[1]
        for i, name in enumerate(list(mcolors.TABLEAU_COLORS))]
    colors = np.empty(voxelarray.shape, dtype = object)
    for p in range(len(pieces)):
        colors[pieces[p]] = all_colors[p]

    # Configure the axes
    ax = plt.figure().add_subplot(projection = '3d')

    ax.voxels(voxelarray, facecolors = colors, edgecolor = 'k')

    # Set axes labels
    ax.set_xlabel('x')
    ax.set_ylabel('y')
    ax.set_zlabel('z')

    # Show the plot
    plt.show()

To get each piece starting from a list of (x, y, z) corrdinates , I’m using the equations below:

# Create a volumetric piece from a piece coordinates matrix
def getPiece(piece_coords):
    # Number of blocks in a piece
    numBlocks = len(piece_coords)

    x, y, z = np.indices((CUBE_SIZE, CUBE_SIZE, CUBE_SIZE))
    x_vals, y_vals, z_vals = piece_coords[ :,X], piece_coords[ :,Y], piece_coords[ :,Z]

    piece_blocks = [(x == x_vals[i]) & (y == z_vals[i]) & (z == y_vals[i]) for i in range(numBlocks)]
    piece = functools.reduce(lambda a, b: a + b, piece_blocks)

    return piece

You might have noticed above that the coordinates for Y and Z are reversed. That’s not a mistake and if we’d use them the expected way, we would get the pieces reversed:

    piece_blocks = [(x == x_vals[i]) & (y == z_vals[i]) & (z == y_vals[i]) for i in range(numBlocks)]

For the rotations, I’m using the 3D rotation matrices above and have created a lambda function to rotate a piece a number of times around an axis:

# Rotation matrixes
R = [
    # Rotate by 90 about the x axis
    np.array([[1, 0, 0], [0, 0, -1], [0, 1, 0]]),
    # Rotate by 90 about the y axis
    np.array([[0, 0, 1], [0, 1, 0], [-1, 0, 0]]),
    # Rotate by 90 about the z axis
    np.array([[0, -1, 0], [1, 0, 0], [0, 0, 1]])
]

# Rotate a piece a number of times
rotate = lambda coords, axis, times: np.dot(coords, matrix_power(R[axis], times))

To make sure I get all the possible rotations, and this is an important bit I didn’t realise in the beginning, it’s not sufficient to rotate a piece around its 3 axes. We need to rotate it around an axis, then for each rotation get all possible rotations. With the power of Python we can do this in just a couple of lines:

    # Brute-force possible rotations
    prod = [p for p in itertools.product(range(4), repeat = 3)]
    rotations = [rotate(rotate(rotate(coords, X, p[X]), Y, p[Y]), Z, p[Z]) for p in prod]

Same trick for generating all the possible translations, with the help of itertools.product to generate all combinations with repetitions of (0, 1, 2):

# Brute force all possible translations
    prod = [p for p in itertools.product(range(3), repeat = 3)]
    translations = [translate(translate(translate(v, X, p[X]), Y, p[Y]), Z, p[Z]) for p in prod for v in valid]

After generating all possible rotations and translations, which result in a valid piece inside the 3x3 cube, I’ve used a naive search algorithm but with some twists. I’ve generated all the valid 2-piece combinations, and then gradually tried to add another piece to the cube. The results are pretty decent: 3-4 seconds for a 6-piece cube and under half a minute for a 7-piece cube:

(env-viz) cubes ➤ time python solver.py pieces1.txt
[*] Unique combinations for piece 0:  48
[*] Unique combinations for piece 1:  96
[*] Unique combinations for piece 2:  96
[*] Unique combinations for piece 3:  96
[*] Unique combinations for piece 4:  96
[*] Unique combinations for piece 5: 144
[*] Found a solution!
python solver.py pieces1.txt  3.22s user 0.41s system 115% cpu 3.145 total
(env-viz) cubes ➤ time python solver.py pieces2.txt
[*] Unique combinations for piece 0:  48
[*] Unique combinations for piece 1:  96
[*] Unique combinations for piece 2:  96
[*] Unique combinations for piece 3: 144
[*] Unique combinations for piece 4:  96
[*] Unique combinations for piece 5:  96
[*] Found a solution!
python solver.py pieces2.txt  4.35s user 0.46s system 114% cpu 4.194 total
(env-viz) cubes ➤ time python solver.py pieces3.txt
[*] Unique combinations for piece 0:  64
[*] Unique combinations for piece 1:  72
[*] Unique combinations for piece 2:  72
[*] Unique combinations for piece 3:  96
[*] Unique combinations for piece 4:  96
[*] Unique combinations for piece 5: 144
[*] Unique combinations for piece 6: 144
[*] Found a solution!
python solver.py pieces3.txt  28.10s user 0.50s system 98% cpu 28.910 total

Optimisations

• One thing that really speeds up the search is to add pieces to the cube in a specific order, starting with the piece with the least valid positions.
• Another thing is to use numpy arrays wherever possible, which are way faster that Python lists. For example when the function that checks if a specific piece is in a list of pieces was writted using lists, the running time jsut for that function was around half a minute. When re-written using numpy arrays, it finished in under 3 seconds. The new variant is also way more clearer:

  # Check if a numpy array (piece) is in a list of arrays
  def isIn(val, list):
    # The blocks of the piece can be in different order in the array
  
    for el in list:
        #print(el)
        if all([row.tolist() in val.tolist() for row in el]):
            return True
  
    return False
  

• Looking at the numbers of possible valid combinations for each piece, and keeping in mind that we’re placing pieces inside a cube, it became obvious that there will be a lot of symmetrical solutions. So if we really want to speed up the solution search we need only to look for the first (or first few) valid position(s) of the first piece).

If you’re interested to play with the code, I’ve uploaded my Python solver with a couple of custom cubes configurations here. Thank you very much for your time reading this and happy puzzle solving!

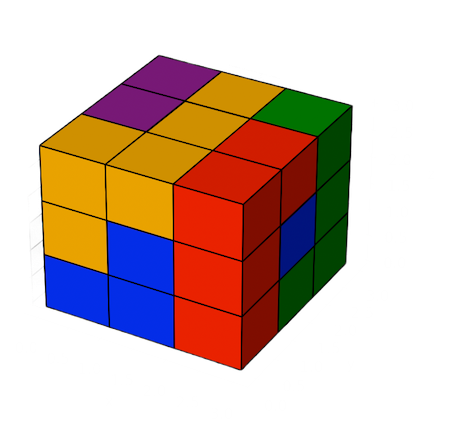
Update: I’ve tweaked the code a bit to work with 4x4 cubes and tested it against a 10-piece 4x4 cube and it found a solution in 16 seconds. I’ve uploaded the pieces configuration here if anyone wants to play with this one too. Enjoy!

References

• Rotation matrixes
• 3D voxel / volumetric plot
• Wooden cube C solver